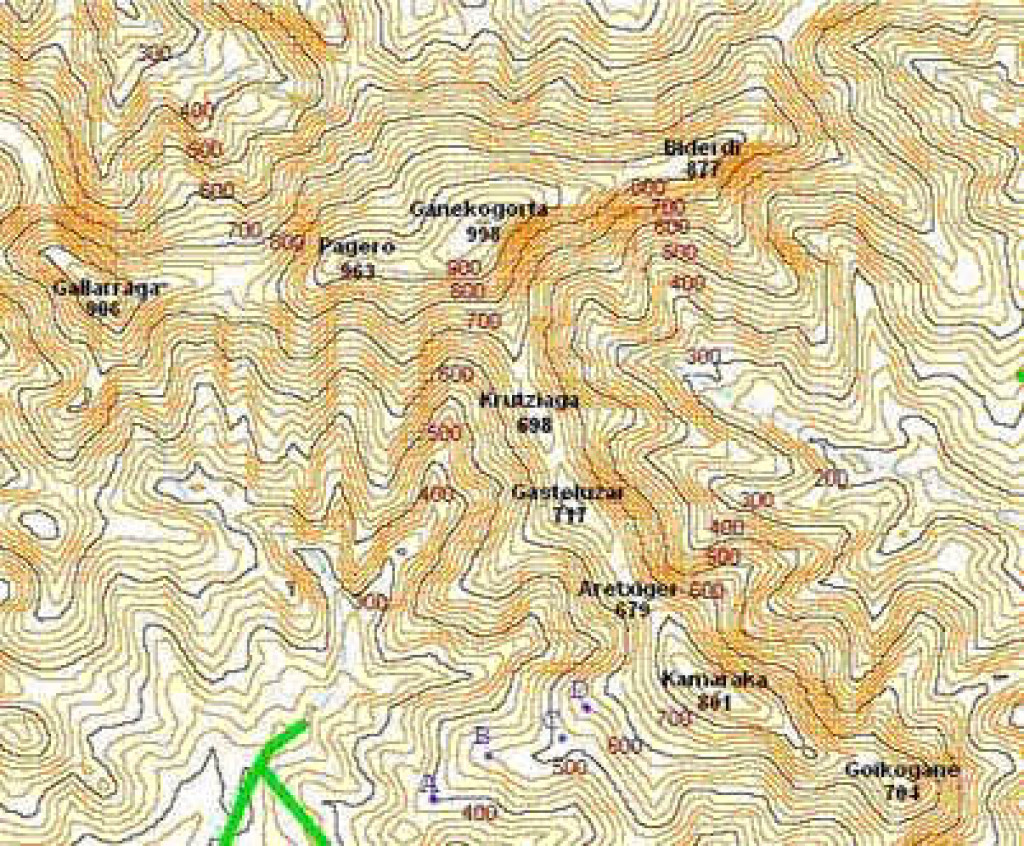
Curvas de nivel
El sistema de representación de curvas de nivel consiste en cortar la superficie del terreno mediante un conjunto de planos paralelos entre sí, separados una cierta distancia unos de otros. Cada plano corta al terreno formando una figura (plana) que recibe el nombre de curva de nivel o isohipsa. La proyección de todas estas curvas de nivel sobre un plano común (el mapa) da lugar a la representación buscada.
En la figura se ve la construcción para representar mediante curvas de nivel una montaña. La montaña es cortada mediante planos paralelos separados una cierta distancia que se llama equidistancia entre curvas de nivel.
Planos equidistantes formando curvas de nivel
Las intersecciones de los planos con la superficie de la montaña determinan un conjunto de secciones que son proyectadas sobre el plano inferior, que representa al mapa. El resultado final que observaremos sobre el mapa es algo como esto:
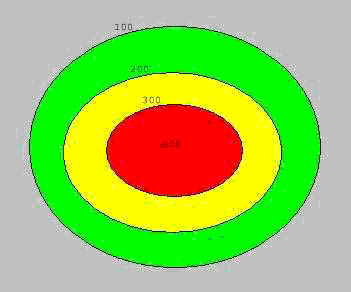
Cortes de los planos proyectados sobre el papel
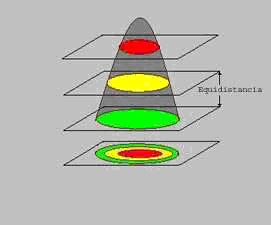
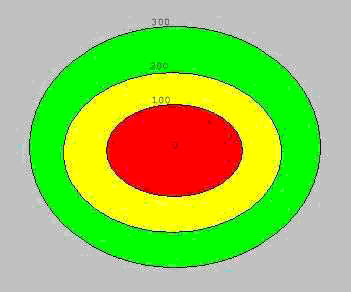
Al observar la figura nos puede quedar la duda sobre qué secciones están por encima de otras. Es decir, ¿está realmente la sección roja por encima de la amarilla y de la verde?
El problema anterior se resuelve fácilmente si para cada sección indicamos su altura con respecto a un plano de referencia, y como tal plano se toma el nivel del mar. De este modo la sección verde se ha obtenido cortando la montaña mediante un plano paralelo al nivel del mar y una altura (o nivel) de 100 metros con respecto a aquél. La sección amarilla se ha obtenido mediante la intersección con un plano a 200 metros sobre el nivel del mar (s.n.m.). Y la sección roja con un plano a 300 metros s.n.m. Para cada curva de nivel indicaremos esa altitud y le denominaremos cota.
La equidistancia entre curvas de nivel se puede deducir ahora con facilidad para el ejemplo dado: 100 metros.
En la siguiente figura se ve como se efectúa la construcción de curvas de nivel de una depresión, que es el caso opuesto al monte de la figura anterior.
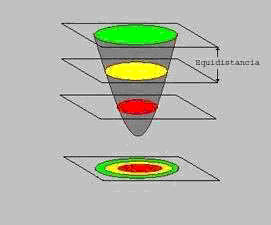
Cortes de los planos proyectados sobre una depresión
Puede observarse que el procedimiento a seguir es exactamente el mismo y que se obtiene la misma representación.
Curvas de nivel de la depresión
Sin embargo, la acotación de las curvas de nivel no dejan lugar a dudas. Podemos observar que las curvas de mayor cota encierran a las curvas de cota menor, señal inequívoca de una depresión en el terreno. En un monte ocurre justo lo contrario, las curvas de nivel de menor cota encierran a las de cota mayor.
Las curvas de nivel verifican las siguientes premisas de manera general:
- Las curvas de nivel no se cortan ni se cruzan (sólo ocurre ésto cuando queremos representar una cueva o un saliente de roca).
- Las curvas de nivel se acumulan en las laderas más abruptas y están más espaciadas en las laderas más suaves.
- La línea de máxima pendiente entre dos curvas de nivel es aquella que las une mediante la distancia más corta.
En la siguiente figura tenemos dos itinerarios para alcanzar una cumbre desde dos puntos A y B. Desde el punto A (itinerario rojo) es más largo que desde el punto B (recorrido azul). Sin embargo, el itinerario azul es mucho más duro ya que las curvas de nivel se hallan más apretadas o, si se prefiere, el camino atraviesa las curvas de nivel en menos espacio.
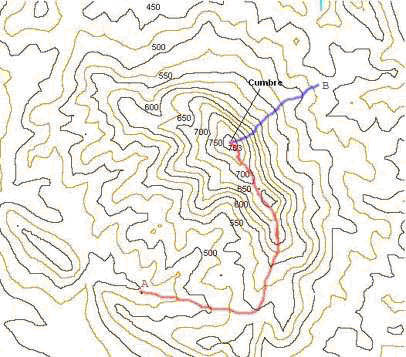
Diferentes itinerarios a cumbre
Equidistancia entre curvas de nivel
La distancia entre los diversos planos imaginarios que cortan el terreno es siempre la misma para un mapa dado y se llama equidistancia entre curvas de nivel.
En el plano anterior la equidistancia entre curvas de nivel es de 25 metros. Obsérvese que se usan dos colores para poder contar mejor las curvas de nivel. Así las líneas más oscuras aparecen cada 50 metros, y entre dos de ellas consecutivas aparece una línea más clara. En cualquier caso entre dos curvas de nivel tendremos una diferencia de altitud de 25 metros. A las líneas más oscuras se les suele llamar curvas de nivel maestras.
Equidistancia entre curvas de nivel
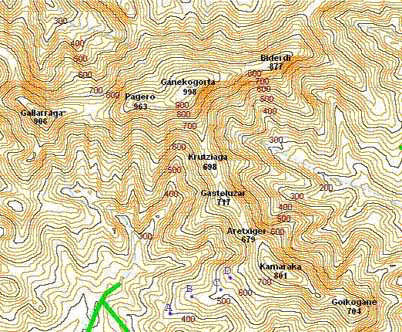
En el nuevo plano tenemos un mapa con equidistancia entre curvas de nivel de 20 metros. Las curvas maestras aparecen en tono oscuro cada 100 metros. Entre dos curvas maestras consecutivas tenemos, por tanto, cuatro curvas de nivel en tono más claro. Entre dos curvas cualesquiera existe una diferencia de nivel de 20 metros.
Cota de un punto
Cada punto de un mapa se sitúa a una altitud definida que se viene a denominar cota. La cota de un punto es la longitud vertical que lo separa del plano de comparación, normalmente el nivel del mar.
En vista al plano anterior podemos ver que la cota del punto A es 400 metros, pues se sitúa sobre la curva maestra de 400 metros. La cota del punto B es 480 metros, pues se halla a cuatro curvas de nivel por encima de la curva maestra de 400 metros (400 + 4 x 20 = 480 m). También se puede determinar su cota observando que está en la curva de nivel anterior a la curva maestra de 500 metros (500 - 20 = 480 m). El punto C se encuentra entre las curvas de nivel 500 y 520 metros. Su cota estará pues comprendida entre estos dos valores pero no lo podemos saber con certeza. En tales caso se puede tomar como valor aproximado el valor medio, 510 metros. Finalmente la cota del punto D es 560 metros (500 + 3 x 20 = 560 m).
La referencia establecida para la medición de altitudes (cotas) constituye, en sí, otro ejemplo de datum (el datum vertical). Cada país tiene definido su propio datum vertical, su propia referencia. Si éste tiene costa se elige algún lugar de la misma, como es en España, Alicante. Los países que no tienen costa transfieren el datum a algún lugar de otro país próximo. Este es el caso de Suiza, por ejemplo, que refiere las altitudes al nivel del mar en Marsella. Uno de los casos más destacados por su magnitud es la diferencia de 2’31 metros que hay entre las altitudes medidas en Bélgica y Holanda. En este caso la discrepancia es debida a que en Bélgica la referencia es el nivel medio más bajo en las mareas de primavera, mientras que en Holanda se toma el más alto.
Curvas de nivel auxiliares
En las regiones muy planas encontramos las curvas de nivel sumamente distanciadas por lo que apenas tendremos información relativa a la topografía del terreno.
Supongamos, por ejemplo, un plano con una equidistancia entre curvas de nivel de 25 metros. Cualquier accidente que sea de menor altura sobre el terreno que 25 m quedará sin representar. Pero bastará un franja rocosa vertical de, por ejemplo, 4 metros, para que nos resulte infranqueable.
Estas dos situaciones nos empujan a aumentar el número de curvas de nivel en ciertas zonas de los mapas añadiendo curvas de nivel de menor equidistancia y que se dibujan entre dos curvas de nivel consecutivas. Reciben, estas curvas, el nombre de curvas de nivel auxiliares.
Las curvas de nivel auxiliares se suelen representar mediante trazos discontinuos. En los mapas de equidistancia entre curvas de nivel de 20m, aparecen entre curvas de nivel consecutivas con una equidistancia de 10 m. Por tanto, si entre las curvas de nivel de 340 y 360 metros de cota se nos muestra una curva discontinua, sabremos que es una curva de nivel auxiliar de 350 metros.
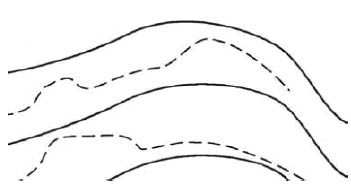
Curvas de nivel auxiliares
Tintas hipsométricas
Un método muy común de representar el relieve en muchos mapas es mediante el método llamado tintas hipsométricas. Este método consiste en dar un color determinado a todos los puntos de un mapa que se sitúan entre dos cotas dadas. Por ejemplo, se puede dar un color verde claro a todos los puntos del mapa con cota comprendida entre 100 y 300 m, verde más oscuro a los puntos con cotas entre 300 y 500 m, amarillo a los puntos con cotas entre 500 y 700 m, etc. Normalmente se usan las tintas hipsométricas como un complemento a las curvas de nivel.
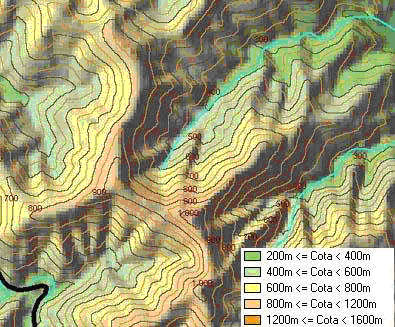
Tintas hipsométricas
En la figura se observa un mapa que usa tintas hipsométricas como complemento a las curvas de nivel (equidistancia de 50 metros) para representar el relieve. En el cuadro anexo se representan los colores usados para cada intervalo de altitudes.
Sombreado
Otro complemento que se usa para la representación del terreno es el sombreado. Consiste en crear unos efectos de sombra e iluminación similar al que originaría un "sol artificial" situado a cierta altitud sobre el relieve.
El sombreado no es una herramienta “cuantitativa” de representación del relieve aunque ayuda en gran medida a su comprensión como superficie tridimensional.
Hay dos sistemas básicos de sombreado:
- Sombreado de Pendiente: Se basa en la cantidad de luz que reciben las superficies en función de su pendiente cuando son iluminadas con un foco de luz situado en la vertical (cenit). Las superficies planas se muestran más claras, pero a medida que ganan inclinación se hacen más oscuras.
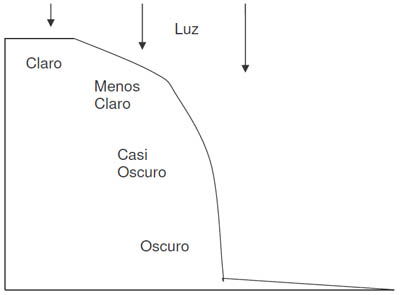
Sombreado de Pendiente
- Sombreado Oblicuo: Es el que se forma cuando un objeto es iluminado mediante un foco de luz situado de forma oblicua con respecto al objeto.
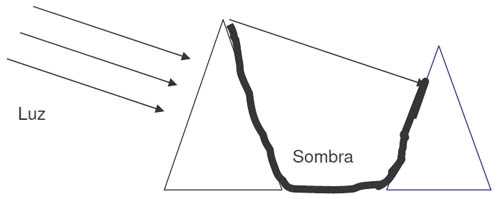
Sombreado oblicuo
El sombreado oblicuo es el más utilizado por ser su interpretación más sencilla. Para utilizarlo hay que empezar por definir la posición del foco de luz imaginario o sol artificial. De forma estándar se suele situar en el ángulo superior izquierdo del mapa (al N.W.) y a una elevación virtual de 45º sobre el horizonte (plano del papel). Por cierto que el Sol nunca alcanza tal posición en el cielo.
Normalmente en los mejores mapas se combina el sombreado con las tintas hipsométricas como herramientas accesorias para la comprensión del relieve.
Extraído del "Curso de Cartografía, Orientación y GPS" de Javier Urrutia. Permitida su reproducción para aplicaciones docentes, culturales y didácticas siempre y cuando éstas no persigan ánimo de lucro ni beneficio particular alguno.
Las curvas de nivel sí se cortan
José Ignacio Montes Lun, 30/12/2013 - 19:32 Enlace permanenteLa ley ;
"Las curvas de nivel nunca se cortan ni se cruzan" es totalmente falsa, solamente se cumple en determinadas figuras geométricas. En el momento en el que exista una cueva, o un volado de roca, las curvas se cortarán y se cruzarán como es obvio.
Es un error demasiado común formular reglas a partir de los hechos más frecuentes y no desde el caso más general y abstracto. Tal y como está planteado en este artículo, la topografía no puede abarcar cualquier superficie de terreno.
Re: Las curvas de nivel sí se cortan
AristaSur Sáb, 04/01/2014 - 17:41 Enlace permanenteHola José Ignacio,
Tienes toda la razón tratarlo como una afirmación sin excepciones, cuando es cierto que si queremos representar una cueva o saliente las líneas se van a cortar. Pero lo normal es representar la altura máxima del terreno, por lo que no suele ocurrir. Hemos modificado el texto para ampliar la afirmación.
Gracias por el aporte.
Hola
fabyyola mondragon Lun, 30/04/2018 - 17:09 Enlace permanenteBuen dia la informacion me fue muy util y es precisa pero tengo una duda voy a citar el documento y necesito el nombre del autor de este documento podrian faiclitarmelo por favor