Barranco del POZALET entre los terminos de Loriguilla y Ribarroja del Turia ambas de (Valencia
El sistema de coordenadas geográficas UTM (Universal Transverse Mercator) se utiliza para referenciar cualquier punto de la superficie terrestre, utilizando para ello un tipo particular de proyección cilíndrica para representar la Tierra sobre el plano.
Vais a necesitar conocer conceptos como la longitud y la latitud, si no los conocéis podéis consultar aquí.
Proyección UTM
Las proyecciones se utilizan para representar un objeto sobre el plano.
La proyección UTM en concreto posee las siguientes características:
- Es una proyección cilíndrica: Se obtiene proyectando el globo terráqueo sobre una superficie cilíndrica.
- Es una proyección transversa: El cilindro es tangente a la superficie terrestre según un meridiano. El eje del cilindro coincide, pues, con el eje ecuatorial.
- Es una proyección conforme: Mantiene el valor de los ángulos. Si se mide un ángulo sobre la proyección coincide con la medida sobre el elipsoide terrestre.
Las ventajas de esta proyección son las siguientes:
- Los paralelos y los meridianos aparecen representados mediante líneas rectas formando una cuadrícula. El sistema de coordenadas pasa de ser esférico a ser rectangular. Resulta sencillo señalar puntos y trazar rumbos entre ellos.
- Las distancias se miden fácilmente. A distancias pequeñas la línea que une dos puntos es una recta (Esto que parece obvio no lo es tanto, si pones los dedos entre dos puntos de una bola del mundo verás que la distancia más corta entre ellos es una línea curva trazada sobre la superficie terrestre).
- Para áreas pequeñas se conserva la forma de los accidentes geográficos sin deformación significativa.
- Los rumbos y las direcciones se marcan con facilidad.
Como principales inconvenientes señalar que:
- No existe una uniformidad en la escala de distancias. Las distancias se agrandan a medida que nos separamos del punto de tangencia esfera-cilindro en la dirección perpendicular al cilindro.
- En latitudes elevadas, alejándonos del punto de tangencia, la deformación es cada vez más importante.
- No se guarda proporción entre las superficies a diferentes latitudes.
- No se pueden representar las zonas polares.

Proyección cilíndrica
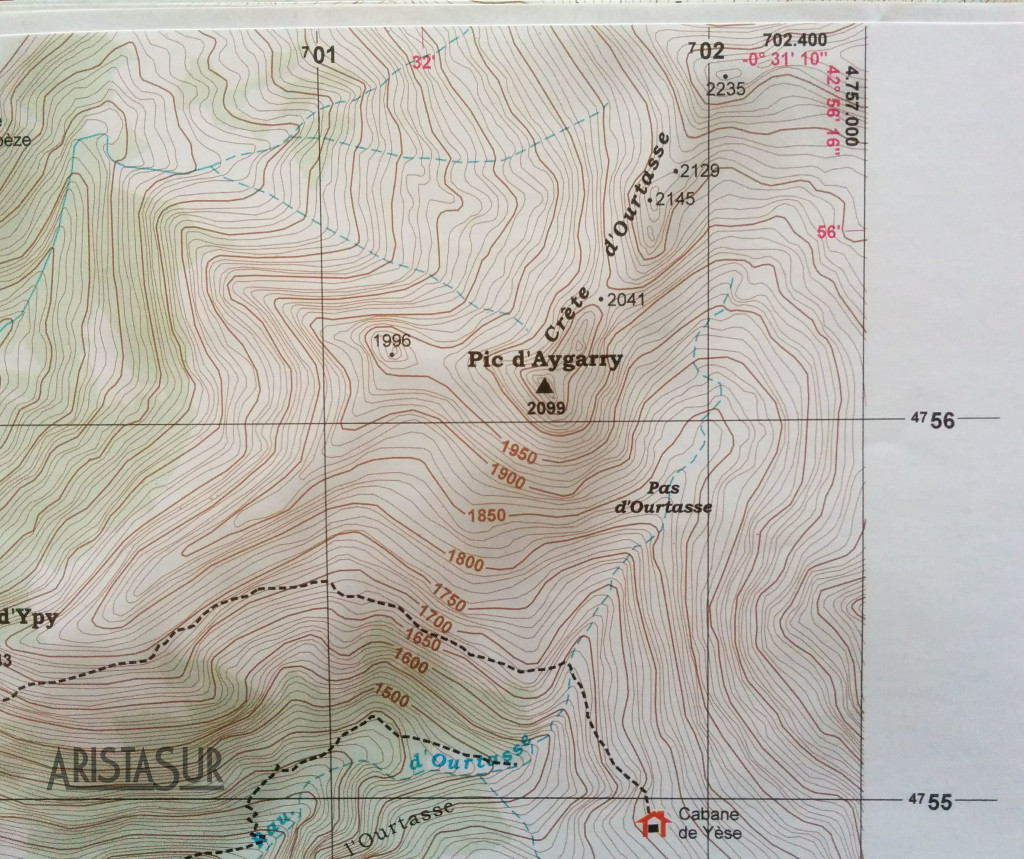
Las siguiente figura muestra el resultado de la proyección U.T.M. sobre el meridiano de Greenwich (en la parte superior el hemisferio correspondiente al antimeridiano 180º y en la parte inferior el hemisferio correspondiente al propio meridiano 0º).
Proyección sobre el meridiano de Greenwich
Estudiándolo un poco podemos ver como aumenta la deformación a medida que nos alejamos del meridiano (centro de la imagen), y como dejan de mantenerse las distancias.
Husos y zonas
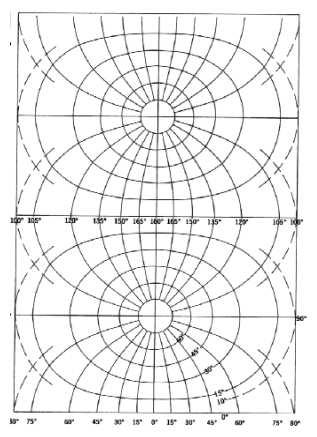
Para resolver el problema de la deformación de la proyección UTM a medida que nos alejamos del meridiano de tangencia lo que se ha hecho es subdividir la superficie terrestre en 60 husos iguales de 6 grados de longitud. Con ello resultan 60 proyecciones iguales, pero cada una con su respectivo meridiano central. Cada huso debe imaginarse como un gajo de una naranja.
Los husos se numeran del 1 al 60 comenzando desde el antimeridiano de Greenwich (180º) hacia el Este. De este modo el huso comprendido entre 180º W y 174º W es el primero.
Cuadrícula husos UTM
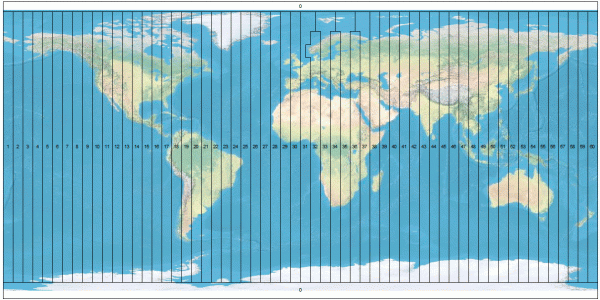
A su vez, dentro de cada huso se establece un división en zonas (o bandas). Cada zona posee 8º de Latitud y 6º de Longitud, y se designa con el número de su huso y una letra mayúscula. Para ello se ha seguido la dirección de Sur a Norte y se ha empezado por la letra C siguiéndose el alfabeto suprimiéndose las vocales y las letras que pueden confundirse con un número (la B, la O y la letra P).
- Las zonas entre la C y la L corresponden al hemisferio Sur.
- Las zonas entre la M y la X corresponden al hemisferio Norte. Como excepción, la zona X posee 12º de latitud y se extiende desde los 72º N hasta los 84º N.
Cuadrícula zonas UTM
La península ibérica queda dentro de 6 zonas: 29T, 30T, 31T, 29S, 30S y 31S.
En ocasiones, no se utiliza la división en zonas anterior, y se realiza una división simple entre zona hemisferio Sur (indicado con una S seguida del huso) y zona hemisferio Norte (indicado con una N seguida del huso). En este caso podemos conocer la zona concreta gracias a la siguiente tabla, ya que sabemos cuántos grados hay de distancia entre cada zona:
| Zona simple | Zona UTM | Rango latitud | Zona simple | Zona UTM | Rango latitud |
| S | C | 72º-80º | N | N | 0º-8º |
| S | D | 64º-72º | N | P | 8º-16º |
| S | E | 56º-64º | N | Q | 16º-24º |
| S | F | 48º-56º | N | R | 24º-32º |
| S | G | 40º-48º | N | S | 32º-40º |
| S | H | 32º-40º | N | T | 40º-48º |
| S | J | 24º-32º | N | U | 48º-56º |
| S | K | 16º-24º | N | V | 56º-64º |
| S | L | 8º-16º | N | W | 64º-72º |
| S | M | 0º-8º | N | X | 72º-84º |
Geometría del huso y ejes cartesianos
Como hemos dicho, cada huso tiene una longitud de 6º (ancho del huso), existiendo un meridiano central a los 3º de longitud que lo divide en dos partes iguales y que se utiliza para la proyección UTM de dicho huso. Además, cada huso está dividido por el paralelo origen Ecuador (alto del huso), que lo divide en dos partes iguales según los hemisferios.
Este meridiano central y el Ecuador son los que van a establecer dos ejes cartesianos en el huso para poder posicionar un punto en toda su superficie. El meridiano central de la zona será el eje Y (vertical), mientras que el Ecuador será el eje X (horizontal).
El eje X tendrá su origen en el meridiano central de la zona, pero tendrá un valor de 500000, disminuyendo hacia el oeste e incrementando hacia el este. Se ha establecido así para tener siempre valores positivos en el eje X.
El eje Y tendrá su origen en el Ecuador, pero lo de hace una manera particular. En el Hemisferio Norte el Ecuador tendrá el valor 0 incrementando hacia el norte hasta llegar al valor 10000000 en el Polo Norte. Mientras que en el Hemisferio Sur el Ecuador tendrá el valor 10000000 decrementando hacia el sur hasta llegar al valor 0 en el Polo Sur. Se ha establecido así para tener siempre valores positivos en el eje Y.
En la siguiente imagen podemos ver los ejes cartesianos y los valores de X e Y.
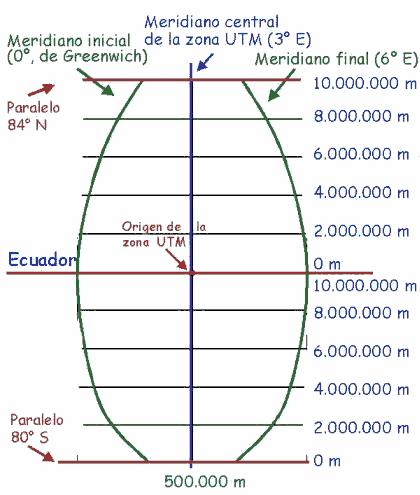
Geometría del huso y ejes cartesianos
Por tanto, debido a esta elección de ejes cartesianos, un punto X y un punto Y referencian una posición en el huso, pero éste es ilocalizable hasta que no se indica en qué huso están y en qué hemisferio.
Con respecto a distancias, cada valor del eje X e Y representa 1 metro en la realidad, por lo que un punto referenciado con estas dos coordenadas nos está haciendo referencia a una zona de 1 metro cuadrado de superficie realmente.
Coordenadas geográficas UTM
Con todo lo anterior, somos capaces de definir una coordenada geográfica en el sistema UTM, compuesta por lo siguientes valores:
Huso Zona Coordenada_X Coordenada_Y
Por ejemplo, el pico Mulhacén tendría la siguiente coordenada UTM:
30S 472313 4100834
Estamos ofreciendo la coordenada con una precisión de metros cuadrados. La coordenada X estará formada por 6 dígitos y la coordenada Y estará formada por 7 dígitos.
Si no necesitamos tanta precisión, podemos dar también la coordenada UTM con una precisión de kilómetros cuadrados. En este caso la coordenada X estará formada por 3 dígitos y la coordenada Y estará formada por 4 dígitos.
30S 472 4100
Además de estos valores, la coordenada debe venir acompañada del Datum de referencia con el que se realizado la proyección, ya que si no el valor puede diferir bastante al posicionarlo sobre un mapa topográfico.
Biblografía
- Curso de Cartografía, Orientación y GPS. Javier Urrutia. Permitida su reproducción para aplicaciones docentes, culturales y didácticas siempre y cuando éstas no persigan ánimo de lucro ni beneficio particular alguno.
- Nomenclatura y cartografía de la proyección UTM de Mercator. Gis and Beers
- Usar las coordenadas UTM en los mapas. The trekking life
Sistema de Coordenadas Geográficas: UTM escrito por AristaSur está protegido por una licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional
